Les points de Lagrange
L’un des aspects de la mécanique céleste qui a occupé mathématiciens et physiciens pendant plusieurs siècles est la recherche de solutions au problème des trois corps, l’analyse du mouvement relatif de trois corps sous l’influence de la force gravitationnelle.
Le cas particulier le plus pertinent est celui où deux corps ont une grande masse et dominent le système, et la masse du troisième corps est négligeable. Ce scénario a des applications très pratiques, puisqu’il fournit une bonne approximation pour calculer la trajectoire d’une sonde autour du système Terre-Lune ou Terre-Soleil. Il permet également d’analyser le mouvement des astéroïdes par rapport au système Jupiter-Soleil ou celui d’exoplanètes autour d’une étoile binaire par exemple.
Le résultat qui nous intéresse ici est la mise en évidence dans un tel système de cinq points particuliers où le troisième corps reste fixe par rapport aux deux premiers. Si l’on considère l’exemple du système Terre-Soleil, il existe ainsi cinq points où une sonde spatiale pourrait être en équilibre (stable ou instable selon le point) et ne pas se déplacer dans le repère défini par la Terre et le Soleil.
Une analyse complète de ce problème a été publiée par le mathématicien et astronome d’origine italienne Joseph-Louis Lagrange en 1772 dans Essai sur le problème des trois corps, d’où le nom donné à ces points.
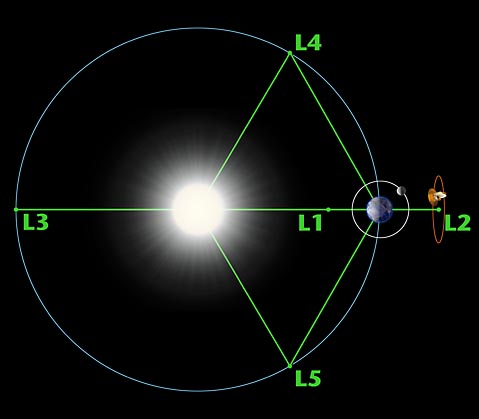
Le point de Lagrange L1
Considérons une sonde spatiale sur une orbite assez circulaire autour du Soleil, mais plus petite que la nôtre, et imaginons le moment où la trajectoire de la sonde passe exactement entre la Terre et le Soleil. Puisque la sonde est plus proche du Soleil que nous, la troisième loi de Kepler indique que sa période de révolution doit être plus courte que la nôtre et la sonde devrait donc rapidement dépasser la Terre.
Mais ne négligeons pas l’effet de la Terre : l’attraction gravitationnelle de notre planète, qui au niveau de la sonde est opposée à celle du Soleil, va compenser une partie de l’attraction de notre étoile. Soumise à une interaction gravitationnelle plus faible, la vitesse orbitale de la sonde va donc être réduite.
En choisissant la position idéale, à environ un centième de la distance Terre-Soleil, soit 1,5 millions de kilomètres, on peut montrer que la vitesse réduite de la sonde conduit à une période orbitale d’une année terrestre exactement. La sonde est donc plus proche du Soleil que nous, mais tourne exactement au même rythme que la Terre. Elle est ainsi figée par rapport au système Terre-Soleil : c’est le point de Lagrange L1.
Le point L1 est instable : si la sonde dévie du point exact, même légèrement, la force de gravité va lentement l’entraîner au loin, vers la Terre ou le Soleil, sans retour possible. Le point L1 ne contient ainsi pas de corps naturels. Cependant, une sonde spatiale possède un système de propulsion et peut donc déjouer cette légère instabilité ou, de préférence, évoluer sur une petite orbite centrée sur le point L1.
Le point L1 du système solaire est un point privilégié pour l’observation du Soleil ou de la face éclairée de la Terre. On y trouve plusieurs sondes spatiales, en particulier l’observatoire solaire SOHO et le satellite d’observation de la Terre DSCOVR, et c’est de là que la sonde LISA Pathfinder a testé les technologies de détection d’ondes gravitationnelles pour la future mission eLISA.
Le point de Lagrange L2
Le point de Lagrange L2 se trouve également sur la ligne Terre-Soleil, mais au-delà de la Terre. Un raisonnement similaire au précèdent s’applique : l’attraction gravitationnelle de la Terre va cette fois s’additionner à celle du Soleil pour accélérer le mouvement d’un corps plus éloigné. A une distance bien déterminée, environ 1,5 millions de kilomètres, un corps aurait la même période orbitale que la Terre et serait donc également figé.
Le point L2, également instable, est un endroit privilégié pour observer l’espace lointain, à l’écart du Soleil et de la Terre mais quand même relativement proche de nous. C’est depuis ce lieu que les satellites WMAP et Planck ont étudié le rayonnement fossile et l’observatoire Herschel l’Univers infrarouge. C’est également de là que l’observatoire Gaia est en train de créer un catalogue d’un milliard d’étoiles, que le télescope spatial James Webb observe l’Univers dans l’infrarouge et que le satellite Euclid mesurera l’accélération de l’expansion de l’Univers à partir de 2023.
Le point L3
Le point L3 se trouve sur la ligne Terre-Soleil, de l’autre côté du Soleil, à une distance légèrement plus faible du Soleil que la Terre. Ce point n’offre guère d’avantage pour l’observation du ciel et présenterait un coût prohibitif, il n’est donc pas exploité. Il aura en tout cas longtemps excité l’imagination des auteurs de science-fiction, puisqu’il aurait fournit un endroit idéal pour cacher une petite planète derrière le Soleil.
Les points L4 et L5
Les points L4 et L5 se déplacent sur la même orbite que la Terre, respectivement devant et derrière notre planète. Vus du Soleil, ils sont séparés de la Terre par un angle de 60 degrés. Contrairement aux précédents, les points de Lagrange L4 et L5 sont dynamiquement stables et sont donc en mesure d’accumuler des corps naturels sur de petites orbites autour du point central.
Ainsi, les points L4 et L5 du système Jupiter-Soleil ont accumulé plus d’un millier d’astéroïdes, appelés des troyens, qui ont été nommés d’après les héros de l’Iliade, les grecs à L4, par exemple (588) Achille, et les troyens à L5, comme (884) Priam.
Le système Terre-Soleil ne possède qu’un astéroïde troyen, 2010 TK7, découvert en 2010 par le télescope infrarouge WISE.
Pour en savoir plus sur les objets et observatoires situés aux points de Lagrange : Wikipédia.
Mis à jour le 24/07/2022 par Dr Olivier Esslinger